A Verified Formal Specification of A Secured Communication Method For Smart Card Applications
Article information
Abstract
In remote villages without access to modern IT technology, simple devices such as smartcards can be used to carry out business transactions. These devices typically store multiple business applications from multiple vendors. Although devices must prevent malicious or accidental security breaches among the applications, a secure communication channel between two applications from different vendors is often required. In this paper, first, we propose a method of establishing secure communication channels between applications in embedded operating systems that run on multi-applet smart cards. Second, we enforce the high assurance using an intransitive noninterference security policy. Thirdly, we formalize the method through the Z language and create the formal specification of the proposed secure system. Finally, we verify its correctness using Rushby's unwinding theorem.
Introduction
Simple devices such as smartcards are highly recommended to execute business transactions for the people without benefits of modern IT technology. A smartcard, for instance, can serve as a prepaid currency and store coupons for flea markets in remote villages. Coupons on the card can be exchanged for currency, whereas currency can be exchanged for coupons.
Multi-applet smart card platforms (Toll et al., 2008; Markantonakis et al., 2017) can host multiple applets (i.e., applications or processes) from many different service vendors. A set of applets from one service vendor is required to be completely separate from that of another service vendor. The complete isolation can be regulated by adopting a noninterference security policy restricting the information flow among some sets of security domains. Once the policy is implemented in the operating system, no applet can communicate with another if their security domains of the vendors are different. If a secure communication channel is required between two applets belonging to different security domains, an intransitive noninterference policy provides a suitable security framework. Intransitive noninterference (INI) security policy allows a mechanism of creating secure communication channels between applications in high assurance embedded operating systems (Rushby 1992; Karger et al., 2000; Schellhorn et al., 2000).
The organization of this paper is as follows: Section 2 presents a few security policies used in our security framework. Section 3 introduces an INI security policy and Rushby’s unwinding theorem which is the foundation of our formal verification of the design. Section 4 describes a set of smart card entities. Section 5 presents a set of smart card commands and proposes a method of creating a secure communication channel between two applets in a high assurance embedded operating system on a multi-applet smart card platform. Section 6 gives a formal proof of the specification. Section 7 concludes the paper.
Security Policies
A mechanism of enforcing a noninterference security policy on computer systems uses mandatory access controls managing which subjects can read or write which objects in the systems (Bell and LaPadula, 1973; Biba, 1977; Denning, 1976; Rushby, 1986). Subjects are applets, applications, or processes and objects are files, directories, or any computer resources producing observable outputs. Each subject is included in a security domain and given a security access clearance. Each object is assigned a security access classification of the security domain that it originates from. Security access clearances and security access classifications are called security tags. A noninterference policy can be enforced by allowing accesses only if certain conditions are met on the security tags.
A lattice security model (Bell and LaPadula, 1973; Denning, 1976; Rushby, 1986) organizes the security to form a partial ordering. An access clearance of a subject is specified by two components of {{access class}, {category}} in a lattice. Set {access class} is a subset of a list of secrecy levels. Set {category} is a subset of a list of compartments. For example, a tag of {{PUBLIC, UNCLASSIFIED}, {HR, ENGINEERING}} represents a security domain where its secrecy level is both PUBLIC and UNCLASSIFIED and its compartment is both HR and ENGINEERING. Note that we do not order the access class in increasing secrecy. We can arbitrarily create tags without considering the order. An access classification of an object is similarly specified and usually inherited from the subject that creates it.
Let tag ST1 be {{AC1}, {CAT1}} and ST2 be {{AC2}, {CAT2}}. ST1 dominates ST2 (denoted by ST1⊇ST2) if {AC1}⊇{AC2} and {CAT1}⊇{CAT2}. Keeping tags secret in a lattice model will promote the system security. Service vendors can create encrypted tags to prevent intruders from guessing them.
The Bell and LaPadula (BLP) secrecy model formalizes two simple properties that defeat a Trojan horse leaking sensitive information (Bell and LaPadula, 1973; Rushby, 1986). The simple security property allows a subject with its access clearance ST1 to read an object with its access classification ST2 if ST1⊇ST2 (no read-up). The security *-property allows a subject with ST1 to write an object with ST2 if ST2⊇ST1 (no write-down).
The Biba integrity model (Biba, 1977) is primarily concerned with malicious modifications of the systems. To protect data from improper modifications of system resources, the model defines integrity tags and two properties that are mathematical duality of BLP’s. An integrity tag is specified by two components of {{access class}, {category}}. Set {access class} is a subset of a list of integrity levels and set {category} is not used in this paper (Karger et al., 2000). The simple integrity property allows a subject with its integrity tag being IT1 to read an object with IT2 if IT2⊇IT1 (no read-down). The integrity *-property allows a subject with IT1 to write an object with IT2 if IT1⊇IT2 (no write-up).
Security domain U is not interfering with domain V (denoted by U≠>V) if no action performed by U can influence subsequent outputs seen by V (Rushby 1992; Schellhorn et al., 2000). Noninterference security policy specifies some set D of security domains and a policy that restricts the allowable flow of information among those domains. A reflexive relation ~> on D is the complement relation of ≠>. U~>V implies that V can access information originated from U. Transitive noninterference security policy simply states that if A~>B and B~>C, then A~>C, where A, B, and C are security domains. The BLP/Biba model is proven to be a realization of the transitive noninterference (TNI) security policy (Rushby, 1992). If A≠>C is specified in a TNI policy and enforced by a BLP/Biba mechanism, information flow from A to C is completely blocked. No B can exist between A and C such that A~>B and B~>C. Intransitive noninterference (INI) security policy can specify A~>B, B~>C, and A≠>C (Rushby, 1992). It allows information flow from A to C via B even if C is completely isolated from A.
Multi-applet smart card platforms can host multiple applets from many different service vendors (Karger et al., 2000; Schellhorn et al., 2000; Toll et al., 2008). A set of applets from one service vendor is required to be completely separate from that of another service vendor. However an applet written for a vendor sometimes requires sending information to another applet written for another vendor. Since INI policy allows information flow from A to C via B even if C is completely isolated from A, we can adopt it to create a secure communication channel between two vendors. A mechanism of enforcing the INI policy and creating a secure communication channel between A and C is presented in this paper.
The Common Criteria is an ISO standard for evaluating an assurance level of a computer security system (Common Criteria, 2017; Toll et al., 2008; Morimoto et al., 2007). It specifies 251 criteria of measuring an evaluation assurance level (EAL) of a secured operating system under test. The highest evaluation assurance level (EAL7) requires a formal high-level design specification of the security policy model implemented in the system and a formal verification of the design specification meeting the conditions of the security policy model. This paper presents a formal design specification of an INI security policy model and a formal verification of the specification.
Z is a formal specification language (Woodcock and Davies, 1996). It is used to produce precise and unambiguous specifications of the functionality of new software system. It is based on set theory and a first-order predicate calculus. The unwinding theorem requires to prove three conditions of the system when an operation is applied (Rushby 1992). These three conditions have a common form of P⇒Q, where P and Q are predicates of the system states, and ⇒ is the implication operation. We choose Z language because of its expressive power of specifying the common form of P⇒Q.
Z/EVES accepts specifications written in Z language and is usd for proving theorems in them (Freitas, 2004; Meisels and Saaltink, 1997). To prove a predicate called the goal to be true, each proof step in Z/EVES transforms the goal into a logically equivalent goal. If the last transformed goal is the predicate true, the proof completes (Rushby, 2013). Z/EVES provides various proof step commands such as the rewrite and reduce command. Users can interactively guide the proof steps using these commands. The ability to control the transformation at each step enables the users to devise proof strategies and detect the source of the failure. We use Z/EVES to verify our formal specifications because of its ability of controlling stepwise transformations. Z/EVES uses automated theorem proving to check if the system satisfies the common form of P⇒Q. It can deal with infinite state space directly and check the system validity for arbitrary input parameters. Another method of commonly used system validation techniques is model checking (Katoen, 1998). It searches the state space exhaustively, therefore is used for verifing a system model with a small finite set of input parameters. This is another reason that we choose to use Z/EVES in this paper.
The Unwinding Theorem
Suppose that subject P executes operation X before subject Q executes operation Y in a machine enforcing the TNI security policy. Let U be a security domain of P and V be that of Q. If U≠>V, then the output of Y seen by Q is not changed if operation X is purged (Rushby 1992). Furthermore if α is a sequence of m operations and α is executed before Q executes Y, any operation Z in α can be purged without changing the output of Y seen by Q if dom(Z) ≠>V where dom(Z) is the security domain of a subject executing Z.
However if a machine implements the INI security policy, Z cannot be purged simply because dom(Z) ≠>V without affecting the output of Y seen by Q. Let W1, W2,…, Wn be a sequence of security domains of n operations in α, where m ≥ n. If W1~> W2~>…~> Wn, W1=dom(Z) and Wn=V, the output of Y seen by Q is indirectly influenced by Z. Z can be purged (called intransitive-purge or ipurge) only if there exists no chain of ~> between dom(Z) and V in a sequence of security domains of α. A machine is secure under an INI security policy if the output of α·Y is the same as the output of ipurge(α)·Y seen by Q.
Information stores in a smart card platform have some internal structure of directories and files (Wolfgang et al., 2003; Java Card, 1998). A state of a system refers to the names and the values of them. Subjects create, read, and write files during their executions. We define a relation U~>V as subject A in domain U writes files and subject B in domain V can read them directly. The system starts at the initial state S0. S0 is defined by initial values of files and directories in the system. The system reaches state S after a sequence of operations α·Y is executed. If we executes another sequence of operations β·Y instead of α·Y, the system reaches another state T which may be different from state S because the final values of the files and the directories of S may be different from those of T. Let dom(Y) be V. We define an equivalent relation S ≈V T if it meets the following condition: every file and directory readable by V in state S is also readable by V in state T and the content of every file and directory in state S is the same as that in state T (Rushby 1992).
When subject B executes Y, it produces outputs. We assume that the outputs are calculated based on the files that B has the right to read. It means that no covert channel can influence the outputs of Y. All references to the files are supposed to be monitored and Y’s outputs depend on the input files readable by B only.
Proving that a system (M) implementing an INI policy is secure requires satisfying the following conditions of Rushby’s unwinding theorem (Rushby 1992; Schellhorn et al., 2000):
1. M is output consistent
2. M is weakly step consistent
3. M locally respects ~>
When a system adopting an INI security policy implements a set of operations, each operation must be tested if it satisfies the three conditions of the unwinding theorem. The operations are often implemented as system calls to an embedded operating system (OS) and their references to information stores are monitored by a mandatory access control to prevent potential information leakage among the security domains specified in the INI policy. We must prove that each system call whose accesses to files are restricted by the mandatory access control indeed satisfies the unwinding theorem.
Smart Card Entities
Multi-applet smart card platforms can host multiple applets from many different service vendors (Schellhorn et al., 2000; Toll et al., 2008; Markantonakis et al., 2017; Wolfgang et al., 2003; Java Card, 1998). A set of applets from one security domain is required to be completely separate from that of another security domain. If two applets belonging to two different security domains need to communicate each other, a secure communication channel must be created between them. The channel uses resources on the smart card platform. The entities representing these resources are modeled in this section. Their formal specifications are expressed in Z language.
1. Applets
Service vendors write applets to provide various services to card users. Applets are submitted to the third party agent which examines the applets. It detects and removes any potential security holes if possible and evaluates applets’ security and integrity levels according to the specification of the Common Criteria. Applet executable files are downloaded to the card if they pass authorization and authentication procedures set by the card issuer. See more details in (Karger et al., 2000; Schellhorn et al., 2000).
We assume that applets have been created and loaded into the card platform. Creating or loading applets does not violate the INI policy because no references to files are made yet. Applets’ security domains are predetermined by the authority. Each applet is put into a predestined security domain and given a security/integrity tag associated with the domain.
We do not order security (or integrity) levels in increasing secrecy (or integrity) so that the levels are arbitrarily created. Keeping levels secret will promote the system security and integrity. Service vendors can create encrypted levels to prevent intruders from guessing them. We declare three basic data types to specify security levels, categories, and integrity levels. These basic types are declared by writing their names between brackets in Z language as follows:
[SecrecyLevel, IntegerityLevel, Category]
Let Ei be an entity of a system where 1≤ i ≤ n. Ei can be a file or a directory. Let VAL(Ei) be the content of Ei. Then a system state S is defined as: S = {VAL(E1), …, VAL(En)} at the time of observation. A system call can change the stored values of the system entities. It triggers a system state transition from state S to state S′ (the next state of S). A sequence of system calls triggers a sequence of state transitions from its initial state to its final state.
Every applet is identified by a natural number called Applet Identifier (AID). Associated with each applet are two tags for read operations and two tags for write operations. AID is a natural number denoted by ℕ in Z language. All natural numbers are not AID’s because there are a finite number of applets in the system. Therefore the association between an AID and a tag is a partial function denoted by ↛ in Z language. Tags are power sets of the basic types. The power set is denoted by ℙ in Z language. The attributes of each applet are an AID and its security clearance tags and integrity tags for read and write operations. The following schema describes applets at state S:

Every applet has a unique AID. Tag relation sub_read_secClear_s stores the security access clearance for read operations. Tag relation sub_read_intLevel_s stores the integrity level for read operations. Similarly tag relation sub_write_secClear_s and sub_write_intLevel_s are defined for write operations.
The vendor applet schema at state S is defined as follows:

To enforce the BLP/Biba properties, each vendor applet must have the following property: the tag relations for read operations must be the same as those for write operations. Otherwise an applet cannot read a file that it creates.
2. Dedicated Files
We call directories Dedicated Files (DF’s) and files Elementary Files (EF’s) in smart card platforms. DF’s are containers of EF’s and other DF’s (Java Card, 1998). The following schema describes DF’s at state S:

Each DF is identified by a natural number called Dedicated File Identifier (DFID). Every DF has a unique DFID. All natural numbers are not DFID’s because there are a finite number of DF’s in the system. Therefore the association between a DFID and a tag is a partial function. Two tag relations defined for each DF are a security access classification (dir_secClass_s) and an integrity level (dir_intLevel_s). Relation dir_children_s stores its children’s Elementary File Identifiers (EFID’s) and DFID’s. Applets create DF’s. We assume that the most significant bit of DFID is set to one, while that of EFID zero. DF’s tag relations are inherited from the applets creating them.
The root DF is the top directory and instantiated during the system initialization. It is owned by the system and stores loadable applet files.
3. Elementary Files
Elementary Files store byte arrays containing the data (Java Card, 1998). Each EF is identified by a natural number called Elementary File Identifiers (EFID). Each EF has two tag relations, namely a security access classification (obj_secClass_s) and an integrity level (obj_intLevel_s). EF’s tag relations are also inherited from the applets creating them. Relation obj_contents_s stores the actual contents of the files. We restrict each content to a natural number which is regarded as a file version number. The file contents are not used for our formal verification. The following schema describes EF’s at state S:

Creating a Secure Channel
Commercial operating systems provide many Inter-process Communication (IPC) methods. Shared files, shared memory, pipes, and message queues are a few examples. However, these IPC methods cannot be used in high assurance embedded operating systems. Sharing resources such as files and memory can be maliciously used to leak information from a high secrecy level applet to a low one. Message queues between two applets from two different security domains are strictly prohibited.
We will use EF’s as means of secured communication channels. However EF’s must not be shared among applets drawn from randomly selected security domains. Let U, V, and W be security domains. INI security policy allows U~>V, V~>W, and U≠>W (Rushby, 1992). It allows information flow from U to W via V even if W is completely isolated from U. To hold a relation U~>V in an INI policy, applet A in domain U can create or write an EF (EF1) in a DF (DF1) and applet B in domain V can read EF1 and DF1 directly. Similarly to hold a relation V~>W in the same policy, applet B in domain V can create or write another EF (EF2) in another DF (DF2) and applet C in domain W can read EF2 and DF2 directly. Since U≠>W, applet C must be prohibited to read EF1 and DF1.
We define A~>B if U~>V and applet A’s security domain is U and applet B’s security domain is V. A≠>C is similarly defined. The BLP/Biba model is proven to be a realization of the transitive noninterference (TNI) security policy (Rushby 1992; Bell and LaPadula, 1973; Biba, 1977; Rushby, 1986). A mechanism implementing the BLP/Biba model guarantees that A~>B and B~>C implies A~>C. A≠>C is not allowed by a TNI policy in this case. To enforce an INI policy and allow A≠>C, B must be broken into two domains within the single applet, D1 and D2 (Rushby 1992; Karger et al., 2000; Schellhorn et al., 2000). They must satisfy the following conditions: U~>D1, D2~>W, and D1≠>D2. D1 is the domain that B uses for read operations. D2 is for write operations. A creates an EF whose security domain is inherited from A. B can read the EF created by A because U~>D1. B processes the information stored in the EF. Then B writes an EF whose security domain is D2. C can read it because D2~>C. Applet B does not strictly comply with the BLP/Biba properties, but that is what INI policies are all about. We call B INI applet. The following schema describes an INI applet at state S:

Variable bid? is the input parameter of AID. Let t be a tuple defined in Z language, t.1 is the first component of the tuple, t.2 the second component, and so on. For example, (sub_read_ secClears bid?).1 represents the first component of the read tag of applet bid?, which is drawn from ℙSecrecyLevel. Also (sub_read_secClears bid?).2 represents the second component of it drawn from ℙCategory. An INI applet is an applet whose domain for read operations is completely separate from the domain for write operations. Let RT be a tag for reading and WT be a tag for writing. Then it satisfies the following condition: ¬(RT ⊆ WT) ∧ ¬(WT ⊆ RT), where ¬ is a negation operator and ∧ is a logical AND operator. It guarantees that an applet in the read domain of an INI applet neither read nor write a file in the write domain of the same INI applet, and vice versa. Schema INIAppletAtState_s specifies this property of an INI applet within which its read tag neither dominates nor be dominated by its write tag.
The system must support the following system calls to create a secure channel: 1) create a DF, 2) create an EF, 3) read an EF, and 4) write an EF. Each system call accepts input parameters and produces outputs as specified in its design specification. A reference monitor (RM) is an operating system component checking every system call to enforce the access control policy. RM implementing the mandatory access control enforces the INI policy by allowing the system calls only if they satisfy the BLP/Biba properties or they are issued by INI applets (Bell and LaPadula, 1973; Biba, 1977). RM should allow each INI applet to read files if it has read access right to the files and to write files if it has write access right to the files.
1. Create a DF
A schema decorated with a prime represents the next state of the system after an operation is executed on the current state in Z language (Woodcock and Davies, 1996). For example, DedicatedFiles′ represents the state after an operation executed on DedicatedFiles. ΔDedicatedFiles is a schema declaring both DedicatedFiles and DedicatedFiles′ as its components. The name of an input parameter of a schema ends with a query (?). The name of an output parameter ends with a shriek (!) in Z language (Woodcock and Davies, 1996).
System call CreateDF_s creates a DF at system state S. Its input parameters are as follows: 1) AID of the creator (aid?), 2) DFID of the target DF (tdid?), and 3) its parent DFID (pdid?). The input applet calls it. It creates the target DF under the parent DF.
The precondition of CreateDF_s is as follows: 1) the creator must be a vendor applet, and 2) it must have read and write access right to the parent DF. Let ST1 (IT1) be an access clearance (an integrity level) of the input applet for read operations. Let ST0 (IT0) be an access classification (an integrity level) of the parent directory. The following conditions must be met for the applet to read the parent DF: ST1⊇ST0 ∧ IT0⊇IT1. The condition of ST1⊇ST0 ensures that the simple security property of the BLP model holds. Likewise that of IT0⊇IT1 ensures that the simple integrity property of the Biba model holds.
The following schema describes the precondition of reading at state S:

Let ST2 (IT2) be an access clearance (an integrity level) of the input applet for write operations. For the applet to write the parent DF, the following condition must be met: ST0⊇ ST2 ∧ IT2⊇IT0. The condition of ST0⊇ST2 ensures that the *-property of the BLP model holds. Likewise that of IT2 ⊇IT0 ensures that the integrity *-property of the Biba model holds. The following schema describes the precondition of writing at state S:

Schema CreateDF_s checks that target DFID tdid? is new and therefore tdid? is not included in any of the DF’s tag and children domains. It also checks that the parent DFID pdid? exists and the target DF is not a child of the parent DF yet. The postconditions of CreateDF_s are as follows: 1) the target DF is created, and 2) it is stored under the parent DF. New DF’s access classification and integrity level are inherited from the creator. Then it adds the target DF to the list of the children in the parent DF. A successful CreateDF_s operation creates the following two tuples:
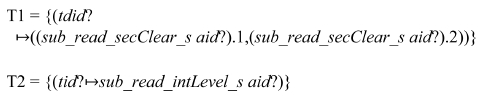
T1 is the access classification of the target DF and added to dir_secClass_s. T2 is the integrity level of the target DF and added to dir_intLevel_s. They are inherited from the creator’s read tags, which are the same as its write tags.
The list of children is stored in dir_children_s. The target DF has no child. So we add tuple {(tdid?→Ø)} to dir_children_s. The parent DF adds {tdid?} to its list of children as follows:
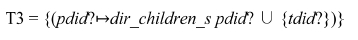
Then it updates in dir_children_s by overriding of itself with T3 using ⊕ operation in Z language (Woodcock and Davies, 1996). The following schema describes CreateDF_s at state S:

2. Create an EF
CreateEF_s system call creates an EF at system state S. Its input parameters are as follows: 1) AID of the creator (aid?), 2) EFID of the target EF (eid?), and 3) its parent DFID (pdid?). The input applet creates the target EF and put it under the parent DF.
The precondition of the system call is as follows: 1) the input applet must be a vendor applet, and 2) it must have read and write access right to the parent DF. The postcondition is as follows: 1) the target EF is created, 2) it is stored under the parent DF, and 3) the content of the EF is set to zero. New EF’s access classification and integrity level are inherited from the creator.
Like CreateDF_s, schema CreateEF_s checks that the target EF is new and the parent DF exists. The tags for the target EF are inherited from the creator. The version number of the target EF is assumed to be zero. Therefore we add tuple {(eid? →Ø)} to obj_contents_s. We do not change dir_secClass_s and dir_intLevel_s because creating an EF does not update the tags of DF’s. Finally we add the target EF to the list of the children in the parent DF.

3. Read an EF
Schema PreCondOfEFReadAccessAtState_s specifies that the simple security property of the BLP model and the simple integrity property of the Biba model hold.

The access clearance of the input applet dominates the access classification of the target EF. The integrity level of the target EF dominates that of the input applet. These properties ensure that the input applet can read the input EF without leaking information.

Schema PreCondOfParentDFContainsEFAtState_s ensures that the target EF is a child of the input directory. The EF must be an element of the power set expressed by dir_children_s pdid? in Z language.

ReadEF_s system call is for reading an EF at system state S. Its input parameters are as follows: 1) AID of the reader (aid?), 2) EFID of the target EF (eid?), and 3) the target EF’s parent DFID (pdid?). The precondition of the system call is as follows: 1) it must have read access right to the parent DF, 2) the parent DF has the target EF as a child, and 3) the applet must have read access right to the target EF. The postcondition is that it returns the content of the EF as the output parameter. Schema ReadEF_s outputs the version number of the input EF through the output parameter out!.
4. Write an EF
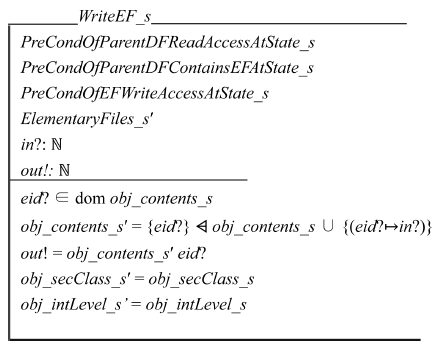
WriteEF_s system call is for writing an EF at system state S. Its input parameters are as follows: 1) AID of the writer (aid?), 2) EFID of the target EF (eid?), 3) the target EF’s parent DFID (pdid?), and 4) the input value to write (in?). The precondition of the system call is as follows: 1) the applet must have read access right to the parent DF, 2) the parent DF has the target EF as a child, and 3) the applet has write access right to the target EF. The postcondition is as follows: 1) the content of the EF is set to the input value (in!), and 2) the value is returned as the output parameter. The access classification and the integrity level of the target EF should not be changed.
Schema PreCondOfEFWriteAccessAtState_s specifies that the security *-property of the BLP model and the integrity *-property of the Biba model hold. The access classification of the target EF dominates the access clearance of the input applet. The integrity level of the input applet dominates that of the target EF.

Schema WriteEF_s checks that the input EF exists. It removes the EF contents using the domain subtraction (?) in Z language from obj_contents_s. Then it adds {(eid??in?)} into it. We do not change obj_secClass_s and obj_intLevel_s because updating the contents of the input EF does not change the tags of it.
Let U, V, and W be security domains. An INI security policy allows U~>V, V~>W, and U≠>W. Applet A, B, and C are from U, V, and W, respectively. A method for creating a secure channel between A and C is as follows: 1) A creates a DF (DF1), 2) A create an EF (EF1) under DF1, 3) C create a DF (DF2), 4) C create an EF (EF2) under DF2, 5) A writes EF1 for sending information to C, 6) B reads EF1, 7) B update EF2, and finally 8) C reads EF2.
A has read and write access right to EF1 and DF1. C has read and write access right to EF2 and DF2. A has no access right to EF2 and DF2. C has no access right to EF1 and DF1. B is an INI applet and has read access right to EF1 and DF1. B has write access right to EF2 and read access right to DF2. RM implementing the BLP/Biba mechanism separates A from C and vice versa. B is the only one INI applet delivering information from U to W in the system. No other applet can leak the information from A to C. Later we will prove that applet B satisfies the three conditions of Rushby’s unwinding theorem, which is the same as proving that the system implementing the method is secure.
B executes step 6 and 7. UpdateINIChannelAtState_s is the body of B’s text area which executes step 6 and 7 at system state S. Its input parameters are the identifiers of DF1, EF1, DF2, EF2, and AID of applet B. The precondition of the applet is as follows: 1) applet B must be an INI applet, 2) B has read access right to EF1, DF1, and DF2, and 3) B has write access right to EF2. The postcondition is as follows: 1) the content of EF1 is returned as an output parameter, 2) the content of EF2 is set to that of EF1, and 3) the content of EF2 is returned as an output parameter. Applet B must run atomically. Every component of Applet_s and DedicatedFiles_s should not be changed at state S during the process. It is expressed in Z language as follows:

ΞSchema includes both Schema and Schema′. And the component values of Schema are the same as those of Schema′ (Woodcock and Davies, 1996). So ΞApplets means that schema Applets is not changed by an operation executed between Applets and Applets′.
Schema UpdateINIChannelAtState_s implements applet B with ReadEF_s and WriteEF_s and renaming their component names as follows:
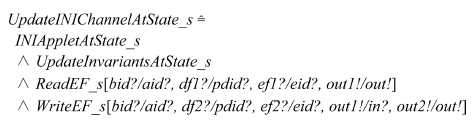
Renaming the components of a schema produces a new schema in Z language. For example Schema[new/old] is the schema produced from Schema by replacing component name old with new (Woodcock and Davies, 1996). Applet B’s AID is bid?. B is an INI applet. B reads EF ef1? in DF df1?. Then it writes EF ef2? in DF df2?. The content of ef1? is set to EF ef2? via the output parameter of ReadEF_s (out1!) and the input parameter of WriteEF_s (in?). Applet_s and DedicatedFiles_s are unchanged.
We assume that DF1 and DF2 are created under the root directory whose DFID is root?. Let AID’s of applet A, B, and C be aid?, bid?, and cid?, respectively. We specify the step 1 through 8 of creating a secure channel as follows:

Input parameter points? of schema AWriteEF1_s is the value of EF ef1? that A writes. Now we describe the sequence of state transitions occurring when we apply step 1 through 8 to the system using schema compositions as follows (Woodcock and Davies, 1996):

Formal Verification of the Method
Proving that a system (M) implementing an INI policy is secure requires satisfying the following conditions of Rushby’s unwinding theorem (Rushby 1992; Schellhorn et al., 2000):
1. M is output consistent
2. M is weakly step consistent
3. M locally respects ~>
To prove that M is secure, we formally specify the equivalence relation S ≈V T which we mentioned in Section 3. We specify new schemas for applets, DF’s, and EF’ at system state T. We will prove that UpdateINIChannelAtState_s system call satisfies the three conditions of the unwinding theorem in this section.
1. Extension of Smart Card Entities
A system state is composed of the names and the values of system entities. A system starts at initial state S0. Each system call triggers a system state transition from one state to the next state. If a sequence of system calls α is applied to the system, the system state may reach state S. Applying another sequence β to the system at S0, the system state may reach another state T. β may be ipurge(α). We define applets, DF’s and EF’s at state T as follows:


New schemas like CreateDF_t, CreateEF_t, ReadEF_t, WriteEF_t, and UpdateINIChannelAtState_t (they are defined on system state T) can be similarly specified. We copy the schemas in the previous sections and rename the components in the schemas so that they refer to state T instead of state S. For example, WriteEF_t is a schema that writes an EF at state T and described as follows:

For another example, schema UpdateINIChannelAtState_t is described as follows:
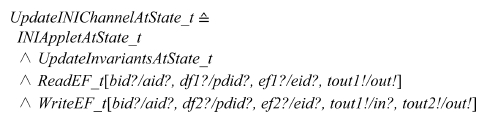
The output parameter of ReadEF_t is renamed to tout1! and that of WriteEF_T is renamed to tout2!.
2. Definition of Equivalence Relation
Let S and T be states of a system and V be a security domain. Let eid be an EFID and VAL(eid, S) be the content of EF eid at state S. P, Q, and R are propositions defined as follows:
P: EF eid is readable in domain V at state S
Q: EF eid is readable in domain V at state T
R: VAL(eid, S) = VAL(eid, T)
We define an equivalent relation S ≈V T as follows: if an EF readable in domain V is chosen at state S, then it is also readable in domain V at state T and the content of the EF at state S is the same as that at state T (Rushby 1992). So we define S ≈V T by ∀eid: ℕ• P ⇒ Q ∧ R, where ℕ is the set of natural numbers and ⇒ is the implication operation. Assume that applet aid? is from domain V and EF eid is stored under DF pdid. The following schema describes ∀eid: ℕ• P at state S:

The schema is used as a predicate representing the set of all EF’s that applet aid? can read. The applet must have read access right to DF pdid and EF eid. EF eid is stored under DF pdid.
The same EF must exist and be readable by applet aid? at state T if S ≈V T. The following schema describes ∀eid: ℕ• Q at state T:

The following schema describes VAL(eid, S) = VAL(eid, T):

If we assume that S ≈V T, then ∀eid: N • P ⇒ Q ∧ R. The following schema describes the equivalence relation between state S and T:

3. Proof of Output Consistency
Let S and T be states and S ≈V T. Let O(op, S) is the output when operation op is applies to the system at state S. A system is output consistent (OC) if S ≈V T ⇒ O(op, S) = O(op, T) (Rushby, 1992).
Let B from domain V be an INI applet. During the execution of UpdateINIChannel_s, applet B reads EF ef1? and sets VAL(ef2?, S) to VAL(ef1?, S). Therefore obj_contents_s of ef2? is replaced by obj_contents_s of ef1?. So obj_contents_s′ is written in Z language as follows:
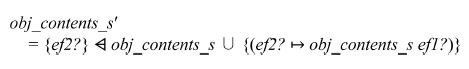
Since VAL(ef2?, S) is set to VAL(ef1?, S), obj_contents_s′ of ef2? is the same as obj_contents_s of ef1?.
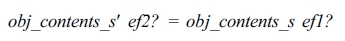
To prove that VAL(ef2?, S′) = VAL(ef1?, S) and VAL(ef2?, T′) = VAL(ef1?, T) where S′ and T′ are the next state of S and T respectively, we write schema Proof_AntiRestriction and prove that it is true.

So the following statements are true and used for proving other theorems:
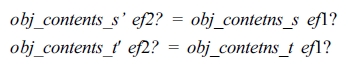
We do not change the characteristics of applets during the system state transitions. Every applet stays in the same security/integrity domain regardless of the system states.

We prove that UpdateINIChannel_s is output consistent as follows:
1) start from two system states S and T such that S ≈V T,
2) apply UpdateINIChannel_s to the system at state S,
3) apply UpdateINIChannel_t to the system at state T,
4) prove that the output of step 2 is the same as that of step 3.
We have proven that the following theorem is true:

UpdateInvariantsAtStates_all in the antecedent of the theorem guarantees that applet B’s security/integrity domain stays the same. We have already proved that VAL(ef2?, S′) = VAL(ef1?, S) and VAL(ef2?, T′) = VAL(ef1?, T). The theorem proves that UpdateINIChannel_s and UpdateINIChannel_t indeed produce the same observable outputs if S ≈V T. Therefore the system is output consistent.
4. Proof of Weakly Step Consistency
Let S′ = Next(op, Y, S) be the next state when an applet from domain Y performs operation op on the system at state S. Then T′ = Next(op, Y, T). A system is weakly step consistent (WSC) if S ≈X T ∧ S ≈Y T ⇒ Next(op, Y, S) ≈X Next(op, Y, T) (Rushby 1992). To specify the precondition of S′≈X T′, we define the following schemas for state S′:

Schema PreCondOfParentDFReadAccessAtState_sprime specifies that the simple security property of the BLP model and the simple integrity property of the Biba model hold at state S′. The access clearance of the input applet dominates the access classification of the target DF. The integrity level of the target DF dominates that of the input applet. These properties ensure that the input applet can read the input DF without leaking information.
We can similarly specify schema PreC ondOfEFReadAccessAtState_sprime and schema PreCondOfParentDFContainsEFAtState_spime as follows:


We can similarly define the following schemas state T′.
PreCondOfParentDFReadAccessAtState_tprime
PreCondOfEFReadAccessAtState_tprime
PreCondOfParentDFContainsEFAtState_tpime
The following schema describes VAL(eid?, S′) = VAL(eid?, T′):

Let P′, Q′, and R′ be propositions defined as follows:
P′: EF eid is readable in domain X at state S′
Q′: EF eid is readable in domain X at state T′
R′: VAL(eid, S′) = VAL(eid, T′)
Then we define S′ ≈X T′ by ∀eid: ℕ • P′ ⇒ Q′ ∧ R′, where ℕ is the set of natural numbers. The equivalence relation between S′ and T′ is defined as follows:

To prove that a system is WSC, we choose two different security domains X and Y. An applet from domain Y executes UpdateINIChannelAtState_s. It makes a state transition from state S to state S′. So Y is V in our context. We have three choices for X. Firstly, if we choose a domain for X which is neither U nor W, then all EF’s readable or writable by domain X will not be affected by the update operation. Therefore S′≈X T′ is trivially proven to be true. Secondly, if we choose domain U for X, U is the security domain of applet A. We should prove that S ≈U T ∧ S ≈V T ⇒ Next(op, V, S) ≈U Next(op, V, T), where op is UpdateINIChannelAtState_s (or _t), which reads EF1 and writes to EF2. Since S ≈U T is assumed, if applet A can read an EF (e.g., EF3) in state S, A can also read it at state T. The content of EF3 at state S is the same as that at state T after the update operation regardless of whether EF3 = EF1 because it reads only EF1. Therefore Next(op, V, S) ≈U Next(op, V, T) holds. Also notice that A is the writer (or producer) for elementary file EF1. Applet A has write access right to EF1 at both state S and T. Let ref? be the EFID of EF3. EF3 may be the same as EF1, which means ref? = ef1?. But ref? ≠ ef2? because EF2 belongs to a different domain (i.e., domain W). The following theorem proves that our implementation of an INI policy is WSC with respect to domain U:

The antecedent of the theorem assumes the followings: 1) applet A has write access right to EF1 at both state S and T, 2) A and B are two distinct applets, 3) EF3 is different from EF2, 4) EF3 exists at both state S′ and T′, 5) the update operation does not change the content of EF3, and 6) S ≈U T ∧ S ≈V T. After applying the update operation on each state, the theorem proves that S′ ≈U T′.
Thirdly, we choose W for X. We should prove that S ≈W T ∧ S ≈V T ⇒ Next(op, V, S) ≈W Next(op, V, T), where op is UpdateINIChannelAtState_s (or _t). W is the security domain of applet C. C is the reader (or consumer) for elementary file EF2. Applet C has read access right to EF2 at both state S and T. Since S ≈W T is assumed, if applet C can read an EF (e.g., EF4) in state S, C can also read it at state T. The content of EF4 at state S is the same as that at state T after the update operation regardless of whether EF4 = EF2 since it writes only EF2. Let ref? be the EFID of EF4. EF4 may be the same as EF2, which means ref? = ef2?. But ref? ≠ ef1? because EF1 belongs to a different domain. If ref? = ef2?, then the update operation sets VAL(ref?, S′) to VAL(ef1?, S) and VAL(ref?, T′) to VAL(ef1?, T). If ref? ≠ ef2?, then the update operation does not change the content of EF4, therefore VAL(ref?, S′) = VAL(ref?, S) ∧ VAL(ref?, T′) = VAL(ref?, T). In both cases Next(op, V, S) ≈w Next(op, V, T) holds.
Theorem Proof_UpdateINIChannel_WSC_wrt_Consumer proves that our implementation of an INI policy is WSC with respect to domain W. The antecedent of the theorem assumes the followings: 1) applet C has read access right to EF2 at both state S and T, 2) C and B are two distinct applets, 3) EF4 is different from EF1, 4) EF4 exists at both state S′ and T′, 4) after the update operation, EF4 at state S’ is the same as that of state T’, 5) S ≈W T ∧ S ≈V T. After the update operation on each state, the theorem proves that S′ ≈W T′.


5. Proof of Local Respect of ~> Relation
Let X and Y be domains. Assume that X≠>Y. A system is locally respect ~> (LR) if an applet from domain X executes an operation at state S, then S ≈Y S′ (Rushby, 1992). Applet B from domain V executes UpdateINIChannel_s in our context. So X is V. We define ≠> relation so that we can assert ¬(V~>Y) as follows:

Schema NegateTildaRelation declares two applets. Applet aid? is a vendor applet. We assume that it is chosen from domain Y. Applet bid? is an INI applet whose domain is V. Applet bid? writes EF2. Therefore the access classification of EF2 dominates the access clearance of applet bid?. The integrity level of applet bid? dominates that of EF2. NegateTildaRelation sets the tags of applet aid? in such a way that it makes applet aid? be unable to read the output (i.e., EF2) from applet bid?. Therefore V≠>Y holds. Let P′′, Q′′, and R′′ be propositions defined as follows:
P′′: EF eid is readable in domain Y at state S
Q′′: EF eid is readable in domain Y at state S′
R′′: VAL(eid, S′) = VAL(eid, S)
The following schema describes R′′:

We define S ≈Y S′ by ∀eid: ℕ• P′′ ⇒ Q′′ ∧ R′′, where ℕ is the set of natural numbers. The following theorem proves that our implementation of an INI policy is LR:

The antecedent of the theorem assumes the followings: 1) V ≠>Y holds, 2) the update operation does not change the content of EF eid (because V≠>Y), and 3) applet aid? from domain Y has read access right to EF eid (i.e., P′′). After the update operation at state S, the consequent of the theorem proves that Q′′ ∧ R′′.
We prove that UpdateINIChannelAtState_s is OC, WSC, and LR in Section 6.3, 6.4, and 6.5 respectively. We can conclude that UpdateINIChannelAtState_s is a system call that satisfies the three conditions of the unwinding theorem. Therefore the system implementing it is secure.
Conclusion
To prove that a system implementing an INI policy is secure, we apply an induction principle to the system states. We prove that 1) the system at initial state S0 is secure, 2) assume that the system at two equivalent state S and T is secure, and 3) executing each system call on the system at state S and T satisfies the three conditions of Rushby’s unwinding theorem (Rushby, 1992; Schellhorn et al., 2000). Proving that the system at S0 is secure is trivial because no reference is made to the system at the beginning.
We defined a set of system calls in Section 5. Among them are CreateDF_s, CreateEF_s, ReadEF_s, and WriteEF_S. We can use the same technique presented in Section 6 to prove that they also satisfy the three conditions of Rushby’s unwinding theorem. Proving them is less complicated than proving UpdateINIChannelAtState_s.
Our approach to a formal design specification and formal verification can be used as a software design process for developing high assurance embedded operating systems.