유한요소해석을 이용한 충격흡수용 마찰 스프링 성능변화 연구
A Study on the Performance of the Shock Absorption Friction Spring using Finite Element Analysis
Article information
Abstract
마찰 스프링은 스프링 내부링과 외부링이 접촉되기 전후의 특성이 달라져 방산, 제철 제강분야 및 우주산업분야 등 다양한 산업에 응용되고 있다. 최근 충격흡수용으로 사용되는 시스템의 경량화와 소형화의 추세에 따라 유압식 완충장치를 대체할 수 있는 마찰 스프링의 사용 빈도가 늘어나고 있다. 본 연구에서는 수직형 완충장치와 같이 충격력을 완화하기 위해 많이 사용되는 마찰 스프링의 성능을 전산해석을 통해 분석하였다. 마찰 스프링을 구성하는 재료의 탄성계수와 링 사이의 마찰계수에 따른 마찰 스프링의 주요 성능인자의 변화를 조사하였다. 이론적 분석을 통해 마찰계수, 탄성계수, 테이퍼각도, 스프링 치수의 함수로 마찰 스프링의 인장강성 및 복귀강성을 나타내는 선행연구 및 시뮬레이션 결과가 유사한 경향을 보임을 확인하였다.
Trans Abstract
The characteristics of friction springs are different before and after the spring is contacted with the inner and outer rings; their applications vary from defense to aerospace industries. Recently, the frequency of using friction springs to replace hydraulic shock absorbers used in high-load areas has been increasing according to the weight reduction and miniaturization of the system. In this research, the performance of friction springs often used to alleviate impact force, such as vertical shock absorbers, was analyzed through computational analysis. Changes in the major performance factors of the friction spring were investigated according to the elastic modulus of the material constituting the friction spring and the friction coefficient between the rings. Through theoretical analysis, it was confirmed that the results of previous studies and simulations showing the tensile and return stiffness of friction springs as a function of friction coefficient, elastic modulus, taper angle, and spring dimensions showed similar trends.
서론
마찰 스프링은 내부링과 외부링이 서로 경사면으로 접촉하도록 교대로 적층하여 사용하게 되며, 압축방향으로만 작동한다. 마찰 스프링의 부하 증가 및 감소의 1회 왕복 과정을 통해서 전달된 충격량의 약 60~70%를 소산시킨다. 또한, 부하가 증가하는 경우와 감소하는 상황에서의 강성 차이 역시 발생하며, 부하가 감소하는 상황에서의 강성이 부하가 증가하는 경우 대비 약 1/3 수준으로 감소한다(Cha, 2010; Cha, 2012). 이러한 특징들로 인해서 방위산업에서 항공우주산업까지 그 적용분야가 다양하다(Cha, 2010).
최근 시스템의 경량화 및 소형화에 따라 마찰 스프링 또한 설치 공간과 부피의 제한을 피하기 위해 소형화 및 경량화 되고 있다. 특히, 고하중 영역에서 사용되는 유압식 충격흡수의 경우 사용환경에 따라 특성변화가 크며, 누유로 인한 유지보수가 어려운 단점이 있어, 이를 대체하여 마찰 스프링을 사용하는 빈도가 늘어나고 있다(Lee, 2017; Cha, 2012). 마찰 스프링의 부하 증가시와 감소시의 강성을 추정하는 연구(Skup, 2007)와, 마찰 스프링의 진동 특성을 분석하는 연구(Cha, 2010), 마찰 스프링의 동역학적 모델링 연구(Gil, 2011), 주퇴복좌기에 마찰 스프링을 적용하는 연구(Cha, 2012), 철근 건축물의 내진 성능 개선에 마찰 스프링을 활용하는 연구(Hu, 2020) 등이 진행되었다. 현재 방위산업, 제강분야, 우주산업(발사체)에서의 충격 흡수용 마찰 스프링의 수요가 증가(Cho, 2011; Oh, 2013)하고 있으므로 국내 개발이 필요한 실정이며, 마찰 스프링의 설계 및 제작을 위하여 성능에 영향을 미치는 인자와 그 관계에 대해서 파악할 필요가 있다.
본 연구에서는 소재의 탄성 계수와 마찰 계수에 따른 마찰 스프링에서의 충격량 소산 성능, 스프링 강성 등을 계산하고 분석하였으며, 향후 마찰 스프링을 설계하는데 있어서 활용될 수 있을 것이라 판단된다.
마찰 스프링
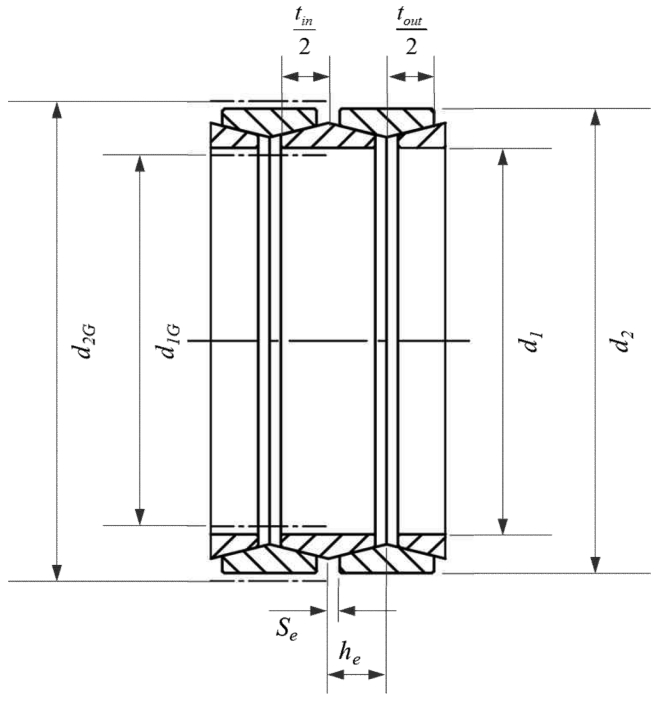
마찰 스프링은 내부 링(inner ring)과 외부 링(outer ring)을 번갈아 위치시켜 구성하며, 그 단면은 Figure 1과 같다. tin과 tout는 내무 및 외부 링의 두께, Se는 내부 링 중심에서 외부링 외각 까지의 거리를, he는 외부링 중심과 내부링 중심 사이의 거리를 나타낸다. d1과 d2는 내부링의 내부지름과 외부링의 외부지름을 각각 나타내며, d1G과 d2G는 마찰 스프링 변형시 내부링의 내부지름, 외부링의 외부지름을 각각 나타낸다.
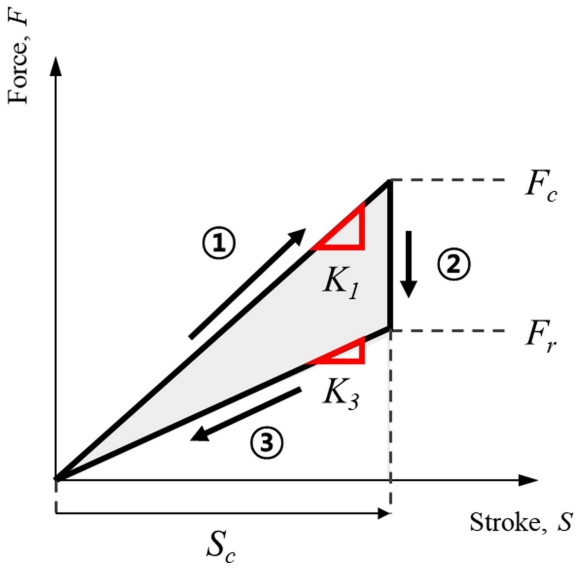
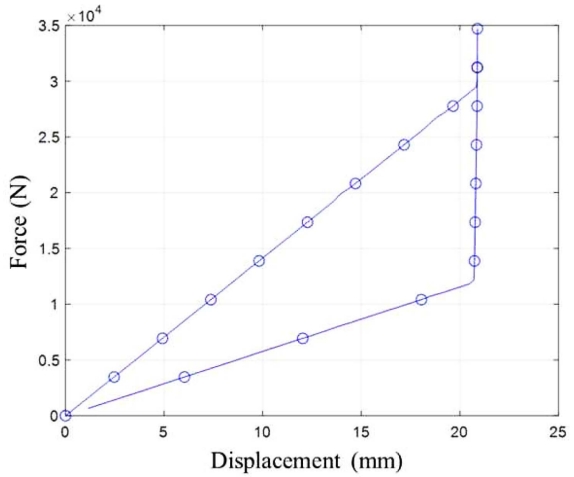
마찰 스프링의 구동 원리는 Figure 2과 같으며 하중(F)이 가해지면, 축 방향의 변위(stroke, S)가 발생한다. 내부 링과 외부 링이 접하고 있는 경사면에서 서로 미끄러짐이 발생한다. 이때, 내부 링과 외부 링은 각각 수축 및 확장한다. Figure 3은 가해진 하중-축 방향 변위 그래프를 나타낸다. 축 하중이 증가하면서 마찰 스프링이 압축되는 과정(①)과 축 하중이 감소하면서 원 상태로 복귀하는 과정(③)가 제시되어 있다. Fc는 마찰 스프링을 Sc 만큼 압축 시킬 때 부여한 하중이며, Fr은 마찰 스프링이 원상태로 복귀하기 시작하는 순간의 복원력을 의미한다.
마찰 스프링에 부하가 증가하는 과정(①)과 부하가 감소하는 과정(③)에서 경사면의 마찰력은 상이하다. 이로 인해서 부하가 증가하는 과정의 강성(Kc)이 부하가 감소하는 과정의 강성(Kr)에 비해 크다. 또한, 압축-복귀 과정에서 마찰로 기인한 에너지 소산이 발생하며, Figure 3에 나타난 폐구간의 영역이 에너지 소산에 해당한다. 마찰 스프링이 압축 시 강성(compression stiffness, Kc)과 원상태 복귀 시 강성(recoil stiffness, Kr)을 힘과 모멘트 평형 방정식을 통해 정리한 결과(Skup, 2007)가 아래와 같다.
여기서, Ai과 Ao는 내부 및 외부 링의 단면적, E는 탄성계수(Young’s modulus), α는 마찰 스프링의 테이퍼 각(taper angle), μ는 내부 과 외부 링 사이의 마찰 계수(frictional coefficient), ri과 ro는 내부 및 외부 링의 평균 반지름, rm = (ri +ro)/2 이다. 또한, 마찰 스프링의 압축 및 복귀 시의 축 하중 및 변위를 이용하여 마찰 스프링의 강성은 아래와 같이 계산될 수 있다.
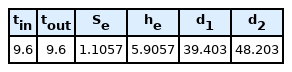
본 연구에 사용된 마찰 스프링은 34 kN 급으로 주요 제원을 Table 1에 나타내었다. 외부 및 내부 링을 각각 9개씩 그리고 절반의 외부 및 내부 링을 각각 1개씩을 적층하여 마찰 스프링을 구성하였다(Figure 4). 마찰 스프링의 소재로는 스프링용 51CrV4를 고려하였으며, 밀도는 8,000 kg/m3, 탄성계수는 210 GPa이다.
전산구조해석
압축 스프링의 압축과 복귀 과정을 상용 시뮬레이션 프로그램인 ANSYS를 이용하여 평가하였다. 마찰 스프링은 축 대칭 형상을 가지고 있으므로, 2차원 축 대칭 모델을 적용하였다. Figure 5에 해석에 사용한 격자(8,771 nodes, 2,569 elements)를 제시하였으며, 압축 스프링 하단과 상단에 각각 변위 및 하중조건을 부여하였다. 링 사이에는 마찰력을 고려하는 접촉 조건(frictional)을 부여하였다.
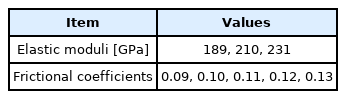
마찰 스프링 재질의 탄성 계수와 마찰 계수에 따른 하중 및 축 방향 변위 결과를 계산하였다. 고려한 탄성 계수 및 마찰 계수를 Table 2에 나타내었으며, 하중에 따른 압축 스프링 상단의 변위를 계산하였다. Figure 6은 탄성계수와 마찰계수가 각각 인 경우의 결과를 나타낸다.
해석 결과
압축 스프링을 구성하는 링의 탄성계수와 링 사이 마찰계수에 따른 압축 스프링의 특성 변화를 살펴보았다. 기존에 힘과 모멘트 평형방정식을 이용하여 이론적으로 압축 강성(Kc)과 복귀 강성(Kr)을 유도한 결과에 따르면, 두 강성값은 탄성계수에 비례하고, 두 강성의 비는 탄성계수에 무관하며 마찰계수에 따라 영향을 받게 된다. Figure 7은 탄성 및 마찰 계수에 따른 압축 강성을 타나낸다. 탄성 및 마찰계수가 증가함에 따라 압축 강성이 증가하는 경향을 나타내었으며, 이는 기존 연구(Skup, 2007)와 동일한 결과이다. Figure 8은 탄성 및 마찰 계수에 따른 압축 강성과 복귀 강성의 비(Kr/Kc)를 나타낸다. 탄성계수는 강성비에 영향을 미치지 않으며, 마찰계수가 증가함에 따라 압축 강성과 복귀 강성의 비가 감소하였다. 시뮬레이션 결과가 기존 연구(Skup, 2007)와 동일한 결과를 나타내었다.
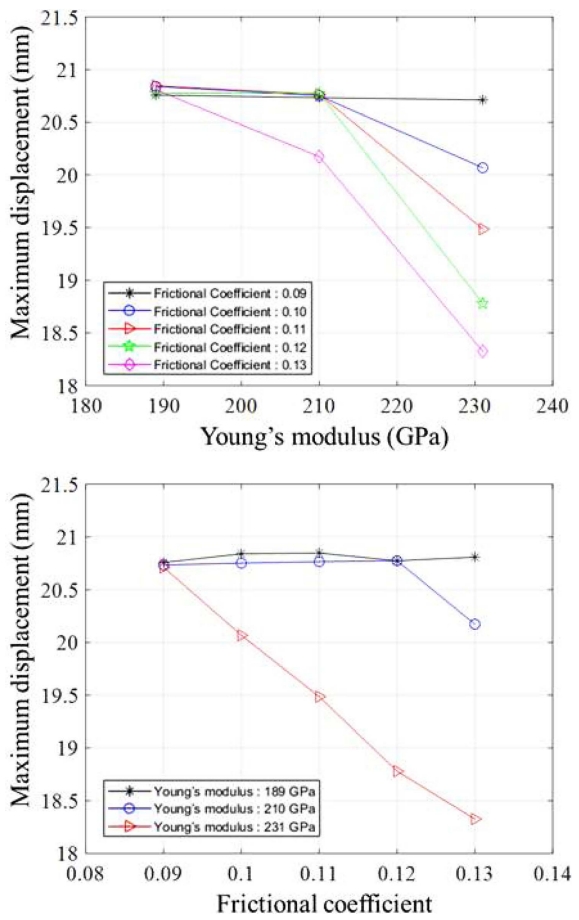
본 논문에서 고려한 압축 스프링은 위아래로 배치된 외부링 또는 내부링 끼리 접촉하게 되면 최대 압축 변위(약 21 mm)가 발생하는 상황이다. Figure 9는 탄성 및 마찰 계수에 따른 최대 변위를 나타낸다. 탄성계수가 가장 작은 경우(189 GPa)에는 모든 마찰 계수에 대해서 34 kN의 하중에 최대 변위가 발생했다. 반면, 탄성계수가 커짐에 따라서 최대 변위가 감소하는 경향을 나타냈다. 또한, 같은 탄성계수에서 마찰계수가 커질수록 최대 변위가 감소하는 경향을 보였다. 이는, 마찰계수와 탄성계수가 마찰 스프링의 압축 강성에 비례하는 경향을 나타내기 때문으로 보인다. Figure 10은 탄성 및 마찰 계수에 따른 충격량 소산을 나타낸다. 동일한 탄성계수에서 마찰 계수가 증가함에 따라 에너지 소산량은 증가한다.
결론
본 논문에서는 수직완충기 등 충격력 완화를 위하여 많이 사용되는 마찰 스프링의 성능을 전산해석을 통해 분석해보았다. 마찰 스프링을 구성하는 재질의 탄성 계수와 링 간의 마찰 계수에 따라서 마찰 스프링의 주요 성능 인자들의 변화를 살펴보았다.
마찰 스프링의 전산구조해석을 위해서 2차원 축대칭 모델을 고려하였으며, 링 간의 마찰 접촉조건 및 적절한 하중/변위 조건을 마찰 스프링 상하단에 부여하였다. 이론적 분석을 통해 마찰 스프링의 인장 및 복귀 강성을 마찰계수, 탄성계수, 테이퍼 각도, 스프링 치수의 함수로 나타낸 기존 연구결과와 시뮬레이션 결과가 유사한 경향을 나타내는 것을 확인하였다.
전산구조해석 결과에서 마찰 계수와 탄성 계수가 마찰 스프링의 압축 및 복귀 강성과 비례하는 것으로 나타났다. 압축 및 복귀 강성의 비는 탄성계수에 무관하며, 마찰계수가 증가함에 따라 압축 강성과 복귀 강성의 비가 감소하였다. 마찰계수가 증가함에 따라서 충격량 소산 역시 증가하였으며, 이는 마찰을 통해 에너지를 소산시키는 마찰 스프링의 원리와 잘 부합하는 결과이다. 상기 결과는 향후 마찰 스프링의 작동 원리를 이해하고 설계하는데 있어서 활용될 수 있을 것으로 기대한다.
Acknowledgements
이 성과는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(NO. NRF-2020R1G1A1006911).